PHD Student: Uday Talwar
Research Problem and Objectives: When a single measurement is on the order of millions of elements, metrics which rely on statistical expectations over high-dimensional stochastic processes are nearly impossible to compute. Even when computational resources are limitless the quantity of sample data can be insufficient to form robust sample statistics required for mathematical observers. Estimating covariance/scatter matrices is a ubiquitous challenge without an obvious solution for high dimension, low sample size (HDLSS) problems. For HDLSS scenarios even simple operations, such as pre-whitening, are intractable because of the reliance on a full-rank covariance estimate. Mathematical observers with robust capabilities to convert high-dimensional, heterogeneous data into information needed for hypothesis testing, data-driven discovery, and causal inferences are sought. Our research focuses on information regarding the detection, classification, or estimation of a signal embedded in heteroscedastic data from multiple sources. In other words, the framework assumes differences in the covariance within one source of data or covariances between different sources as potentially informative. Linear transforms are used to form robust estimates of HDLSS covariance, thus increasing the application span of rigorous mathematical observers.
Focus: How can one optimally perform dimension reduction while minimizing classification error? Channelized data is related to the original data by an underdetermine linear transform that reduces the quantity of elements. In this channelized representation the estimation of higher-order statistics from finite training data becomes possible when the reduction is great enough. In essence, given a data vector ![]() what matrix T reduces the quantity of elements to its optimal channelized representation:
what matrix T reduces the quantity of elements to its optimal channelized representation:![]()
Simulated images from different classes
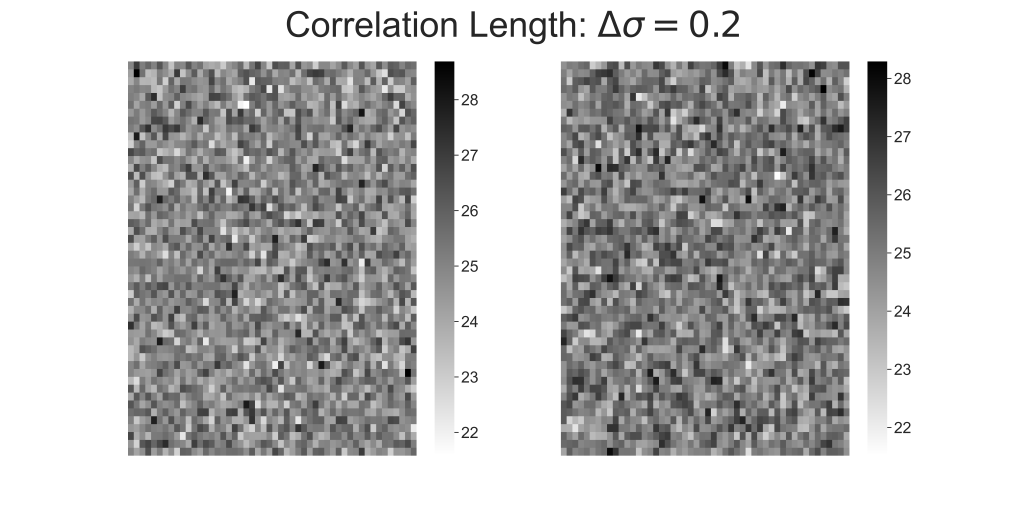
(Left) Image generated from class 1 compared to (Right) image generated from class 2, with correlation length = 0.2 pixels
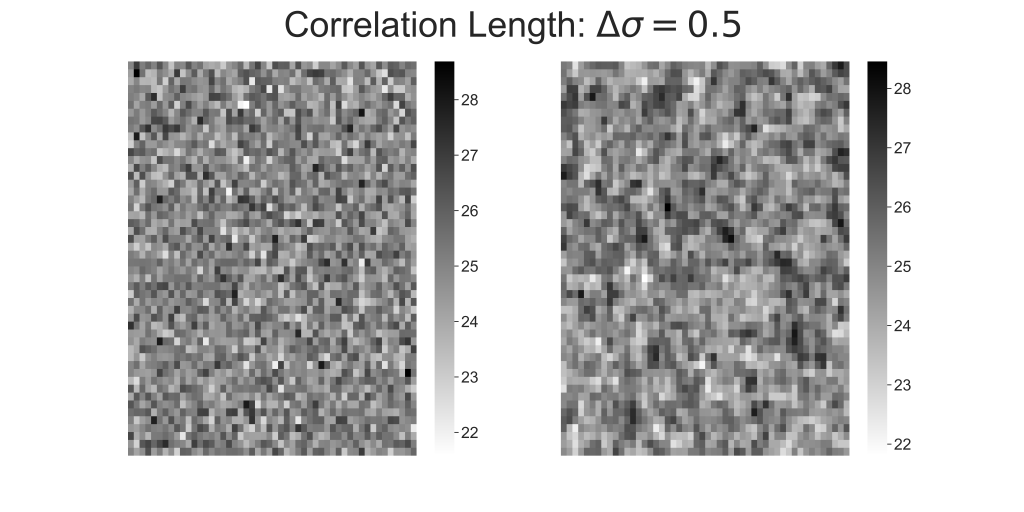
(Left) Image generated from class 1 compared to (Right) image generated from class 2, with correlation length = 0.5 pixels)